動いている車両同士の衝突の衝撃
自動車の損傷や変形の程度から衝突速度を推定できる
交通事故において車両に残された破損や変形の程度から衝突時の車両の速度が分かると、とても便利です。実際に、自動車をいろいろな速度で固定された壁に衝突させて破損や変形と衝突速度の関係を調べる実験が行われています。

自動車が固定壁に衝突する速度と衝突後の変形量については、以下のような関係があることが分かっています。
【式その1】 衝突速度から変形量を予想する場合
変形量(cm)=衝突速度(km/h)×0.95
【式その2】 変形量から衝突速度を推定する場合
衝突速度(km/h)=変形量(cm)×1.05
例えば、衝突による自動車の変形量が40cmであれば、【式その2】によって、
衝突速度(km/h)=40×1.05=42
となるので、衝突速度は時速42キロだったと推定できます。
固定壁への激突速度と自動車の破損・変形の関係について、下の記事でも説明しています。ご覧ください。
動いている車同士の衝突ではどうなるのか?
もっとも、多くの交通事故では、動かない壁に自動車がぶつかるのではなく、動いている車両同士が衝突します。
動いている車両同士の衝突の場合についても、車両の破損や変形と衝突車両の速度との関係が分かると便利ですが、実は、そういったケースについても、固定された壁に車両が衝突したケースに置き換えて考えることができます。
具体的な例でお話しします。簡単な例から考えていきましょう。
同じ速度(例えば50km/h)で走行する2台の同一車種の自動車(車重1.2トン)が正面衝突したとします。下図のケース①です。同一車種なので、2台の重量は同じです。
ケース①の場合と、固定された壁に同じ速度(50km/h)で1台の自動車(同じく1.2トン)が衝突した場合(ケース②とします)では、どちらが紫の車が受ける衝撃が大きいでしょうか?
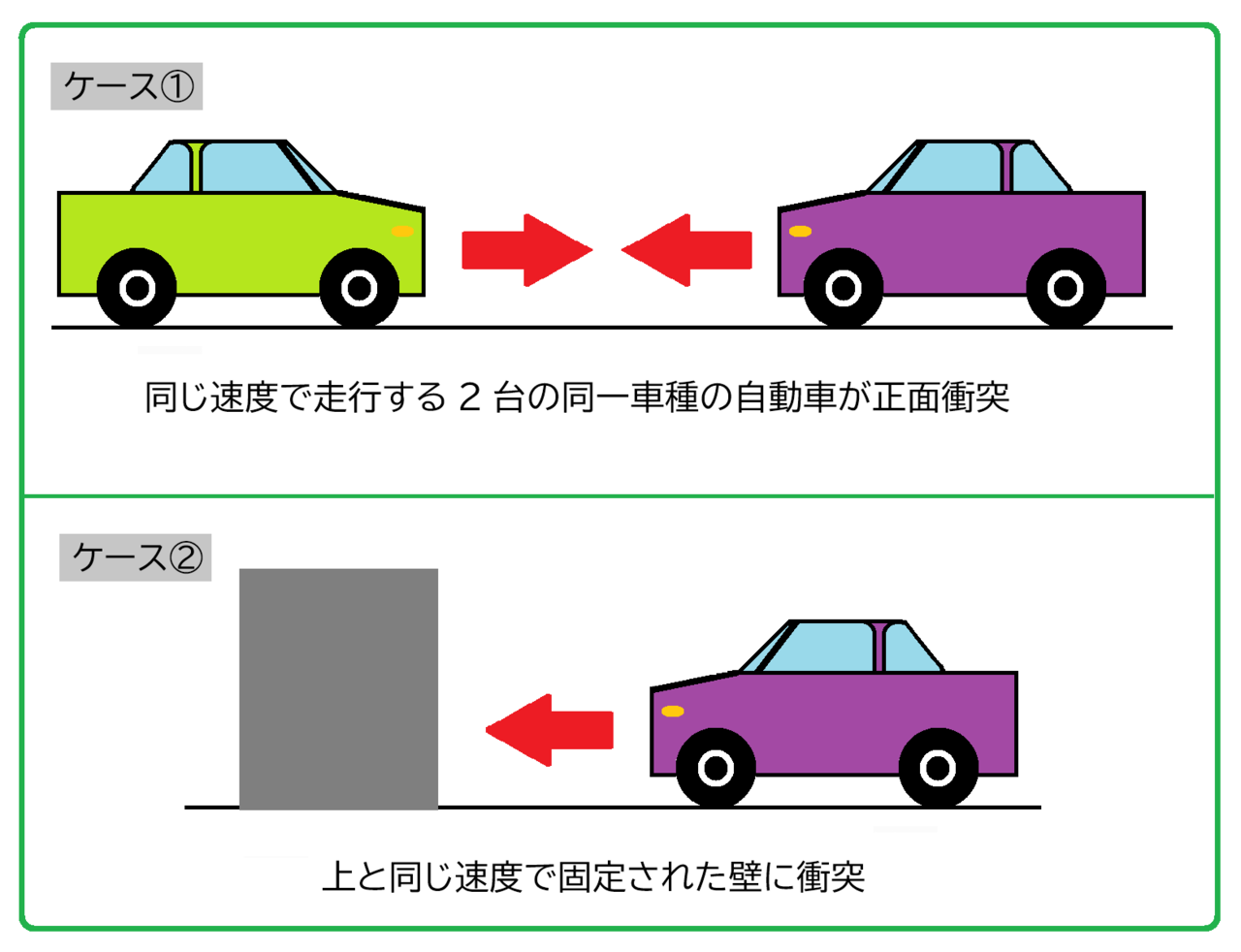
直感的には、固定された壁にぶつかるケース②の場合よりも、対向する車両と正面衝突するケース①の方が衝撃が大きい気がします。
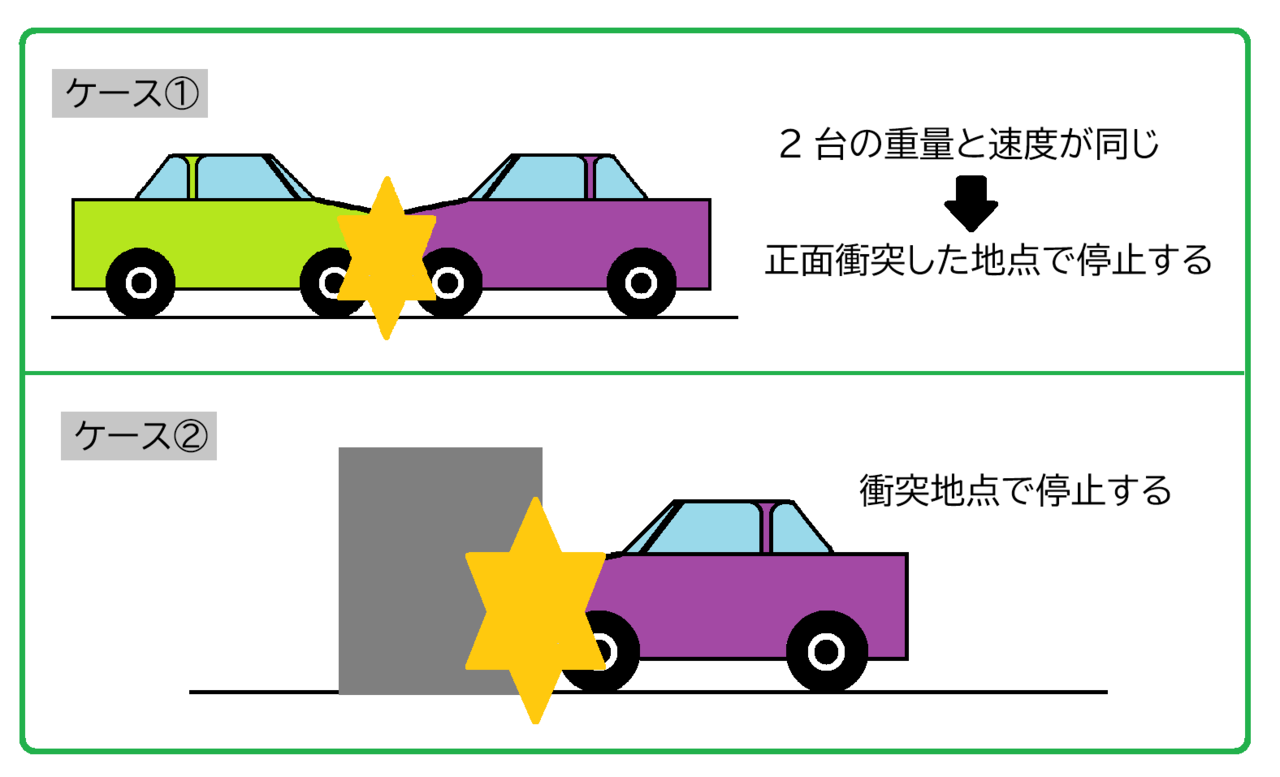
しかし、どちらの場合も、同じです。
ケース①とケース②、どちらの場合でも、紫の自動車は衝突の瞬間に速度が50km/hから強制的に0km/h(つまり停止状態)まで減速させられます。そこで、紫の自動車が受ける衝撃やダメージの大きさは同じと考えることができます。
動いている自動車への追突の場合
続いて、動いている自動車への追突事故について考えます。
分かりやすいように、追突される側の自動車も追突する側の自動車も同一車種とします。
時速80キロで走行する自動車(重量1.2トン)が時速40キロで走行する車両(重量1.2トン)に衝突したと仮定しましょう。下図のケース③です。
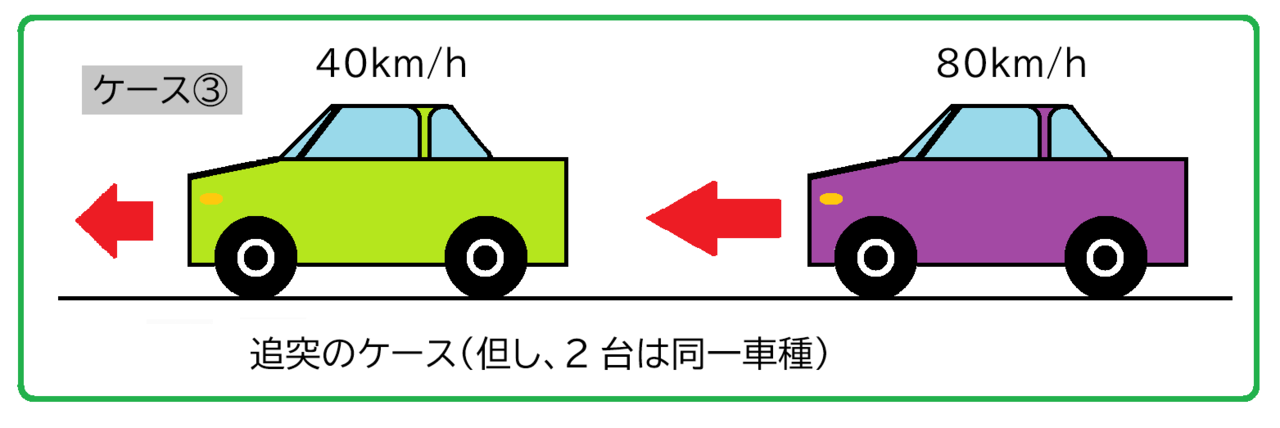
ケース③では、追突後、双方が一体となった時の速度は、60km/hとなります。
双方の車両の重量が同じなので、前方車両の速度40km/hと後方車両の追突前の速度80km/hを平均した速度60km/hが追突後の速度になります。
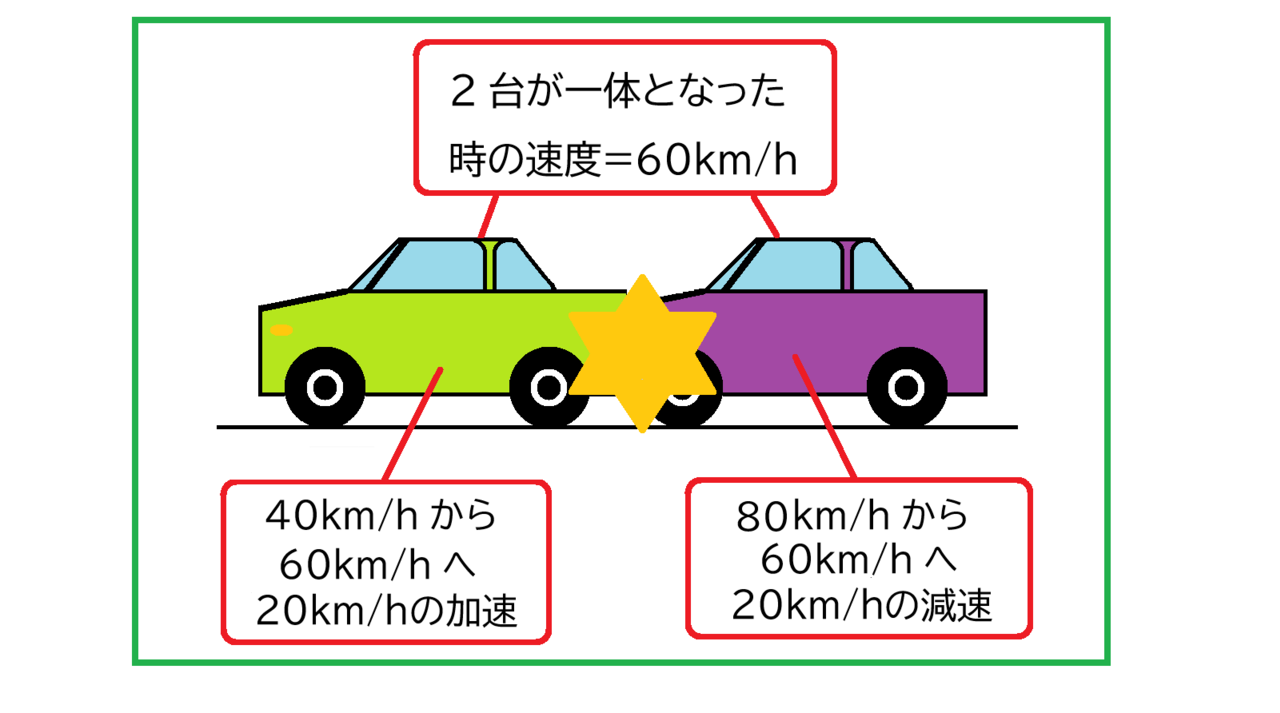
したがって、紫の自動車は、衝突により80km/hから60km/hへと20km/hの減速をします。また、黄緑色の自動車は後ろから衝突されて40km/hから60km/hへと20km/hの加速をします。
そこで、ケース③も下のように置き換えて考えることができます。
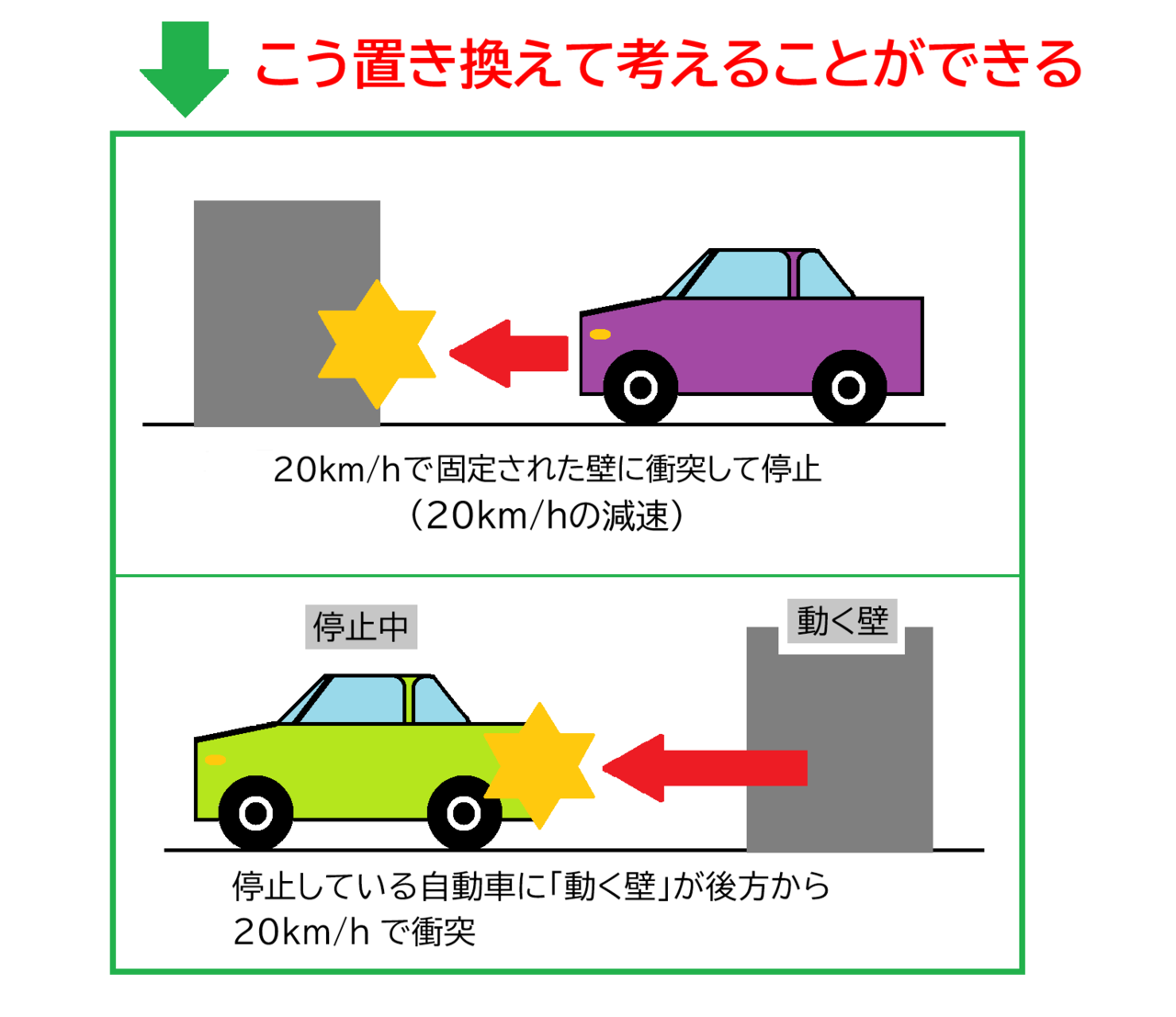
紫の自動車が「衝突により速度が20km/h減速した」については、「20km/hで固定壁に衝突して停止した」と置き換えるのです。
なお、黄緑の自動車については、壁が動いて停止している自動車に衝突するというのも不自然ですので、下のように、「自動車が20km/hで後退して固定された壁に衝突して停止した」と、更に置き換えて考えます。
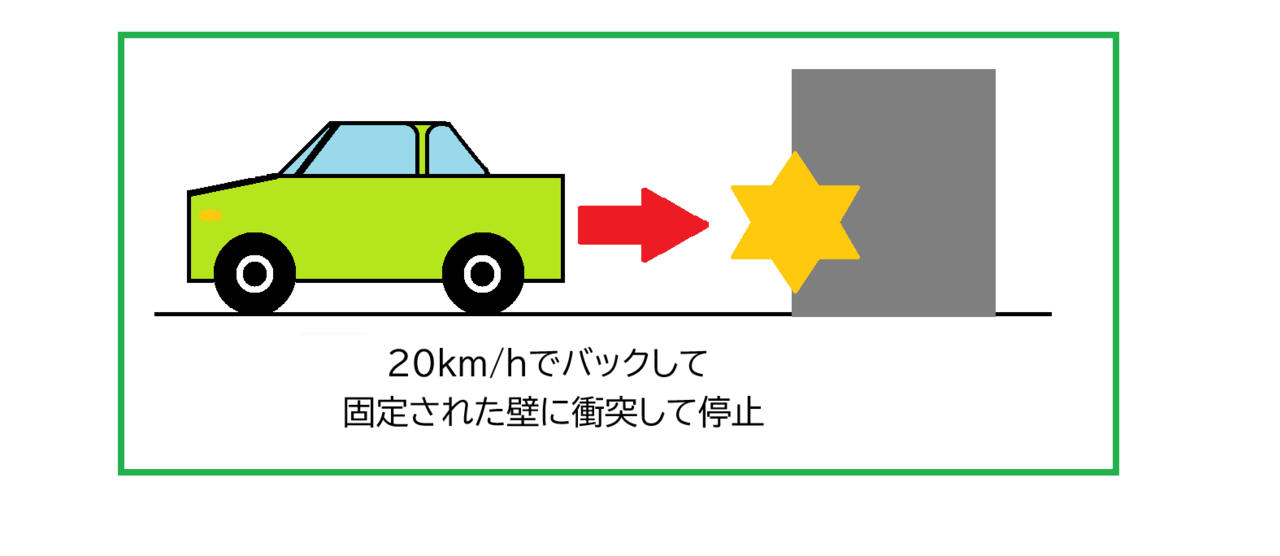
このように、衝突による速度変化→固定壁への衝突速度と置き換えることができるのです。
この置き換えで、動いている自動車同士の衝突についても、固定された壁に衝突した場合に置き換えて考えることが可能となるのです。
このようにして置き換えられた速度のことを、「有効衝突速度」あるいは「バリア換算速度」と呼びます。

重量が異なる車両への追突について
ケース③では、簡単にするために追突する車両もされる車両も、どちらも同じ重量の同一車種としました。
しかし、実際には、追突する側と追突される側の車両はそれぞれ、重量が異なる場合が多いでしょう。
そこで次に、重量が異なる車両同士の追突事故について検討します。
90km/hで走行する1.2トンの自動車が、30km/hで走行する2.4トンの自動車に衝突したというケースを考えます。下図のケース④です。
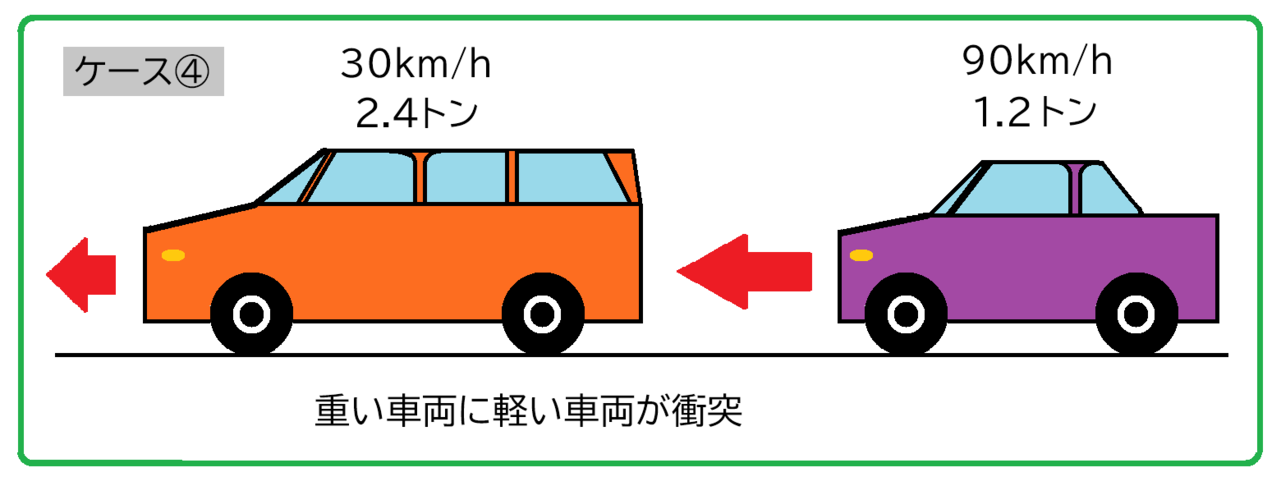
追突後、2台の自動車の速度はどのように変化するのでしょうか。
ケース④では追突する自動車と追突される自動車では重量が大きく異なりますが、衝突によって追突した車両、追突された車両、それぞれの車両の速度がどのように変化するのかは、各車両の重量によって決まります。
下の図をご覧ください。
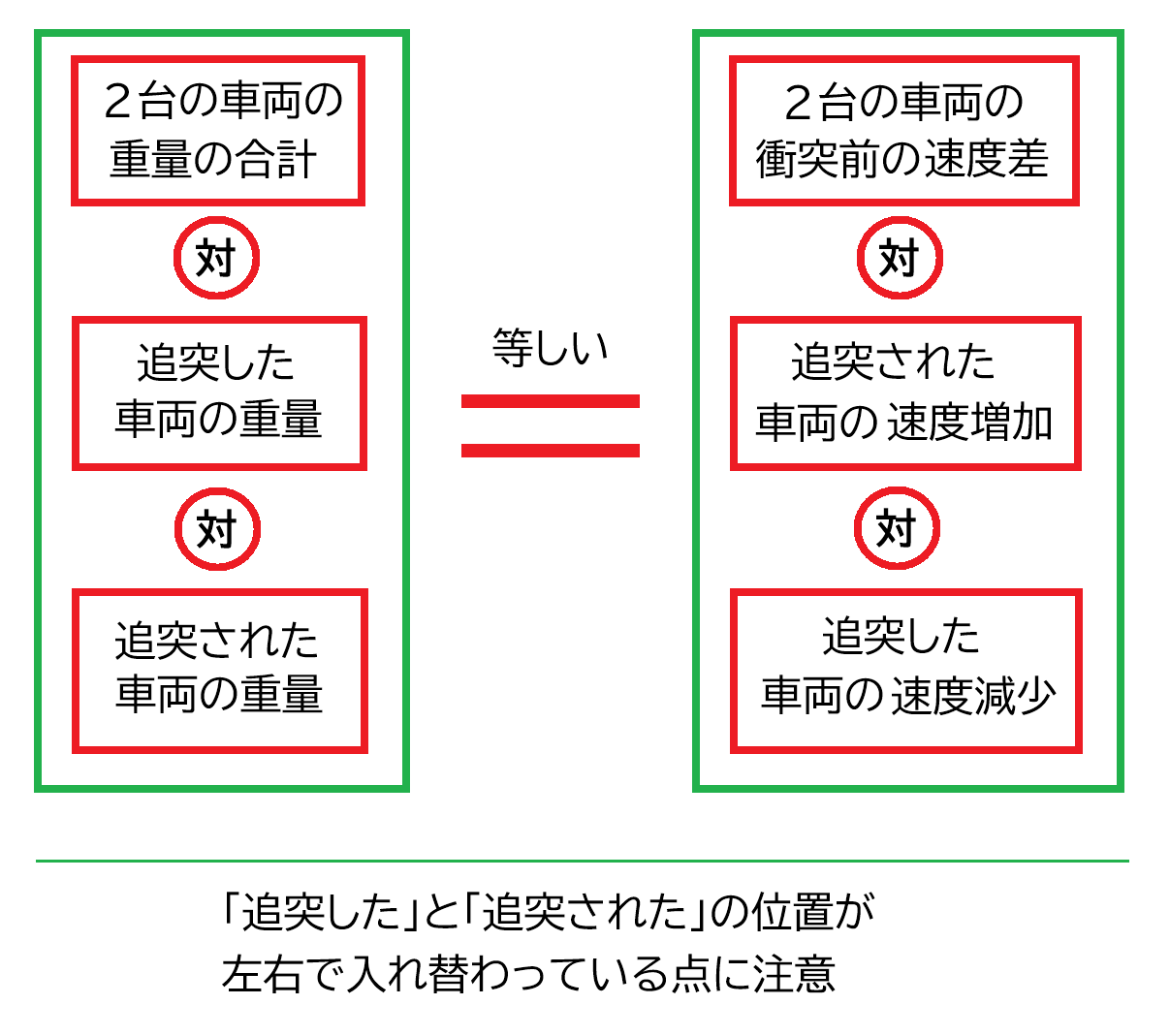
ケース④では、2台の車両の重量合計、追突した車両の重量、追突された車両の重量、それぞれ、3.6トン、1.2トン、2.4トンとなります。
したがって、上の公式に従うと、
「2台の車両の重量合計」:「追突した車両の重量」:「追突された車両の重量」
=「2台の車両の衝突前の速度差」:「追突された車両の速度増加」:「追突した車両の速度減少」
=3.6:1.2:2.4
=3:1:2
となります。
ケース④では、追突による車両の速度変化は以下の通りになります。
衝突前の2台の速度差は60km/ h(90km/h-30km/h)です。
衝突された車両の速度減少は20km/h、衝突した車両の速度減少は40km/hです。
これで、
「2台の車両の衝突前の速度差」:「追突された車両の速度増加」:「追突した車両の速度減少」
=60:20:40
=3:2:1
となります。
したがって、追突した車両は90km/hから40km/hの速度減少をして50km/hとなります。
一方、追突された車両は30km/hから20km/hの速度増加をして50km/hとなります。
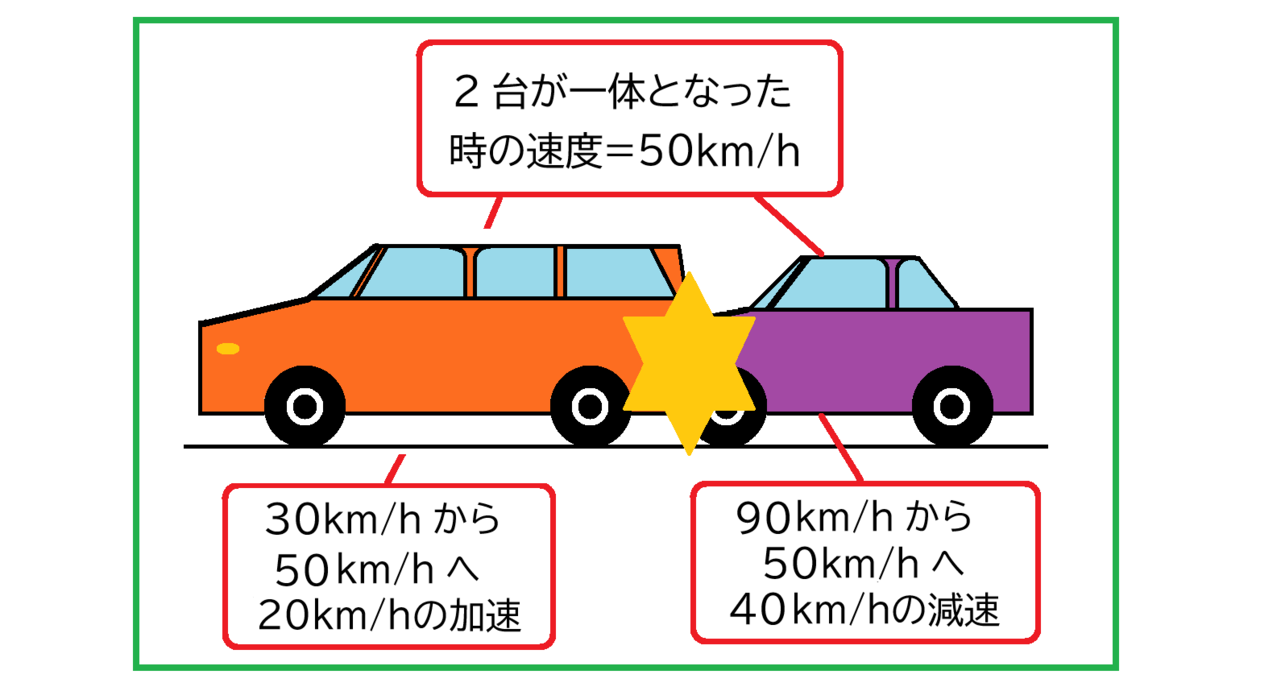
このように、ケース④についても、追突した車両の速度減少、追突された車両の速度増加がわかると、以下の通りに置き換えて考えることができます。固定された壁に衝突した場合に置き換えて考えることが可能となるのです。
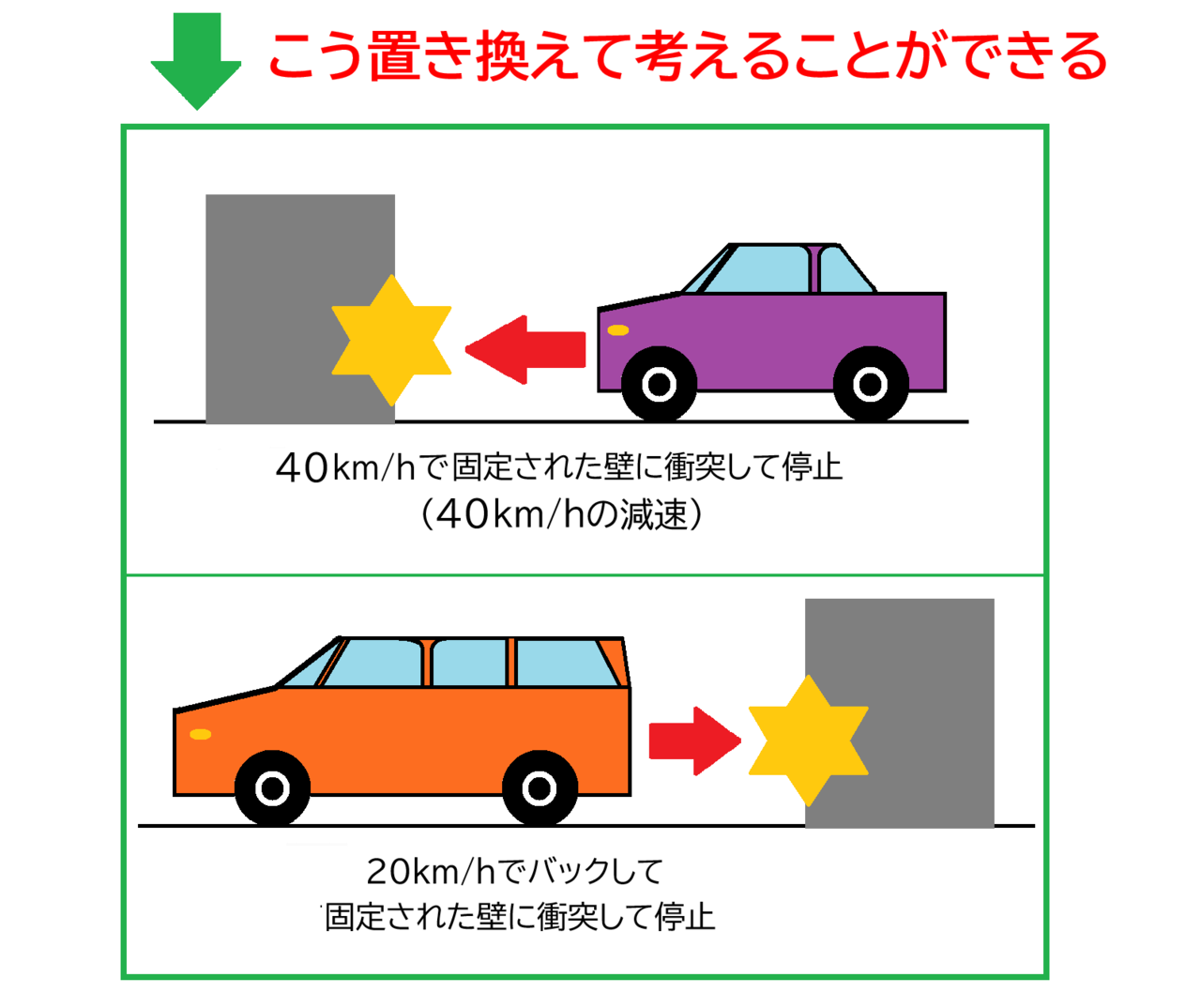
追突車両の変形量から衝突前の2台の速度差を求める
この考え方を使うと、追突後の自動車の変形量から、追突前の2台の車両の速度差を求めることができます。
ケース④と同様に、1.2トンの紫の車両が2.4トンのオレンジの車両に衝突したというケースで考えましょう。仮に、追突した紫の車の変形量が38cmだったとします。
この記事で紹介済みの【式その2】の衝突速度(km/h)=変形量(cm)×1.05を使うと、固定壁に衝突したと仮定した場合の衝突速度=38×1.05=約40km/hとなります。
これは、追突した車両の速度減少とみなすことができます。
したがって、追突した車両が1.2トン、追突された車両が2.4トン、2台の合計重量が3.6トンであれば、
「2台の車両の重量合計」:「追突した車両の重量」:「追突された車両の重量」=「2台の車両の衝突前の速度差」:「追突された車両の速度増加」:「追突した車両の速度減少」=3:1:2
となることから、
2台の車両の速度差=追突した車両の速度減少÷2×3
=40km/h×1.5
=60km/h
となります。
なお、自動車の変形の大きさから衝突速度を求める方法については、以下の記事についてもご覧ください。
示談交渉や訴訟になった場合の流れについては以下を参照ください。
法律相談のご予約はこちら

- 当事務所でのご相談、ご依頼には、弁護士特約を利用できます。
- ご家族が加入している弁護士特約も利用できる場合があります。
法律相談のご予約はお電話にて受け付けております。
受付時間:10:00~18:00
定休日:土曜・日曜・祝日
Menu
- 事務所紹介
インフォメーション
ご相談の予約
ご相談の予約はお電話にて承ります。
受付時間/定休日
受付時間
10:00~18:00
定休日
土曜日・日曜日・祝日
アクセス
〒336-0025
埼玉県さいたま市南区文蔵2-1-2 コルティーレI 302号
